 N and is
formed by evaluating the following summation for each element:
N and is
formed by evaluating the following summation for each element:
![[DBPP]](2_8 Case Study Computational Chemistry_files/asm_color_tiny.gif)





![[Search]](2_8 Case Study Computational Chemistry_files/search_motif.gif)
Our third case study, like the first, is from computational science. It is an example of an application that accesses a distributed data structure in an asynchronous fashion and that is amenable to a functional decomposition.
Computational techniques are being used increasingly as an alternative to experiment in chemistry. In what is called ab initio quantum chemistry , computer programs are used to compute fundamental properties of atoms and molecules, such as bond strengths and reaction energies, from first principles, by solving various approximations to the Schrödinger equation that describes their basic structures. This approach allows the chemist to explore reaction pathways that would be hazardous or expensive to explore experimentally. One application for these techniques is in the investigation of biological processes. For example, Plate 6
shows a molecular model for the active site region in the enzyme malate dehydrogenase, a key enzyme in the conversion of glucose to the high-energy molecule ATP. This image is taken from a simulation of the transfer of a hydride anion from the substrate, malate, to a cofactor, nicotinamide adenine diphosphate. The two isosurfaces colored blue and brown represent lower and higher electron densities, respectively, calculated by using a combined quantum and classical mechanics methodology. The green, red, blue, and white balls are carbon, oxygen, nitrogen, and hydrogen atoms, respectively.
Fundamental to several methods used in quantum chemistry is the need to
compute what is called the Fock matrix, a two-dimensional array representing the electronic structure of an atom or
molecule. This matrix, which is represented here as F, has size
N  N and is
formed by evaluating the following summation for each element:
N and is
formed by evaluating the following summation for each element:
where D is a two-dimensional array of size N  N that
is only read, not written, by this computation and the I represent
integrals that are computed using elements i , j , k
, and l of a read-only, one-dimensional array A with
N that
is only read, not written, by this computation and the I represent
integrals that are computed using elements i , j , k
, and l of a read-only, one-dimensional array A with 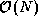 elements. An
integral can be thought of as an approximation to the repulsive force between
two electrons.
elements. An
integral can be thought of as an approximation to the repulsive force between
two electrons.
Because Equation 2.3
includes a double summation, apparently 2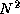 integrals must be
computed for each element of F, for a total of 2
integrals must be
computed for each element of F, for a total of 2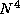 integrals. However, in practice it is possible to exploit redundancy in the
integrals and symmetry in F and reduce this number to a total of
integrals. However, in practice it is possible to exploit redundancy in the
integrals and symmetry in F and reduce this number to a total of 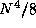 . When this is
done, the algorithm can be reduced to the rather strange logic given as
Algorithm 2.3. In
principle, the calculation of each element of F requires access to all
elements of D and A; furthermore, access patterns appear
highly irregular. In this respect, the Fock matrix construction problem is
representative of many numeric problems with irregular and nonlocal
communication patterns.
. When this is
done, the algorithm can be reduced to the rather strange logic given as
Algorithm 2.3. In
principle, the calculation of each element of F requires access to all
elements of D and A; furthermore, access patterns appear
highly irregular. In this respect, the Fock matrix construction problem is
representative of many numeric problems with irregular and nonlocal
communication patterns.
For the molecular systems of interest to chemists, the problem size
N may be in the range 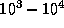 . Because the
evaluation of an integral is a fairly expensive operation, involving
. Because the
evaluation of an integral is a fairly expensive operation, involving 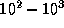 operations, the
construction of the Fock matrix may require
operations, the
construction of the Fock matrix may require 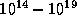 operations. In
addition, most methods require that a series of Fock matrices be constructed,
each representing a more accurate approximation to a molecule's electronic
structure. These considerations have motivated a considerable amount of work on
both efficient parallel algorithms for Fock matrix construction and improved
methods that require the computation of less than
operations. In
addition, most methods require that a series of Fock matrices be constructed,
each representing a more accurate approximation to a molecule's electronic
structure. These considerations have motivated a considerable amount of work on
both efficient parallel algorithms for Fock matrix construction and improved
methods that require the computation of less than 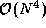 integrals.
integrals.
Because the Fock matrix problem is concerned primarily with the symmetric
two-dimensional matrices F and D, an obvious partitioning
strategy is to apply domain decomposition techniques to these matrices to create
N(N+1)/2 tasks, each containing a single element from each matrix (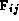 ,
, 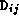 ) and responsible
for the operations required to compute its
) and responsible
for the operations required to compute its 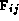 . This yields
N(N+1)/2 tasks, each with
. This yields
N(N+1)/2 tasks, each with  data and each
responsible for computing 2
data and each
responsible for computing 2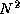 integrals, as specified in Equation 2.3.
integrals, as specified in Equation 2.3.
This domain decomposition strategy is simple but suffers from a significant disadvantage: it cannot easily exploit redundancy and symmetry and, hence, performs eight times too many integral computations. Because an alternative algorithm based on functional decomposition techniques is significantly more efficient (it does not perform redundant computation and does not incur high communication costs), the domain decomposition algorithm is not considered further.
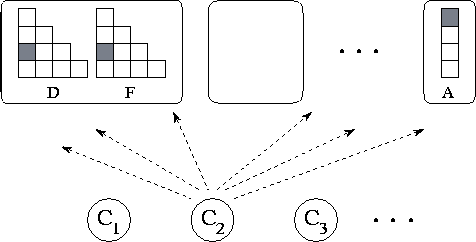
Figure 2.31: Functional decomposition of Fock matrix
problem. This yields about 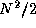 data tasks, shown
in the upper part of the figure, and
data tasks, shown
in the upper part of the figure, and 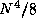 computation
tasks, shown in the lower part of the figure. Computation tasks send read and
write requests to data tasks.
computation
tasks, shown in the lower part of the figure. Computation tasks send read and
write requests to data tasks.
Quite a different parallel algorithm can be developed by focusing on the
computation to be performed rather than on the data structures manipulated, in
other words, by using a functional decomposition. When redundancy is considered,
one naturally thinks of a computation as comprising a set of integrals (the
integral procedure of Algorithm 2.3), each
requiring six D elements and contributing to six F elements.
Focusing on these computations, we define 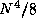 ``computation''
tasks, each responsible for one integral.
``computation''
tasks, each responsible for one integral.
Having defined a functional decomposition, we next need to distribute data
structures over tasks. However, we see no obvious criteria by which data
elements might be associated with one computation task rather than another: each
data element is accessed by many tasks. In effect, the F, D,
and A arrays constitute large data structures that the computation
tasks need to access in a distributed and asynchronous fashion. This situation
suggests that the techniques described in Section 2.3.4 for
asynchronous communication may be useful. Hence, for now we simply define two
sets of ``data'' tasks that are responsible only for responding to requests to
read and write data values. These tasks encapsulate elements of the
two-dimensional arrays D and F (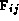 ,
, 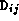 ) and of the
one-dimensional array A (
) and of the
one-dimensional array A (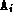 ), respectively.
In all, our partition yields a total of approximately
), respectively.
In all, our partition yields a total of approximately 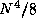 computation tasks and
computation tasks and 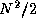 data tasks
(Figure 2.31).
data tasks
(Figure 2.31).
We have now defined 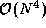 computation tasks
and
computation tasks
and 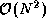 data tasks. Each computation task must perform sixteen
communications: six to obtain D matrix elements, four to obtain
A matrix elements, and six to store F matrix elements. As the
computational costs of different integrals can vary significantly, there does
not appear to be any opportunity for organizing these communication operations
into a regular structure, as is advocated in Section 2.3.2.
data tasks. Each computation task must perform sixteen
communications: six to obtain D matrix elements, four to obtain
A matrix elements, and six to store F matrix elements. As the
computational costs of different integrals can vary significantly, there does
not appear to be any opportunity for organizing these communication operations
into a regular structure, as is advocated in Section 2.3.2.
On many parallel computers, the cost of an integral will be comparable to the cost of a communication. Hence, communication requirements must be reduced by agglomeration. We describe two alternative strategies that can be used to achieve this goal. Their data requirements are illustrated in Figure 2.32.
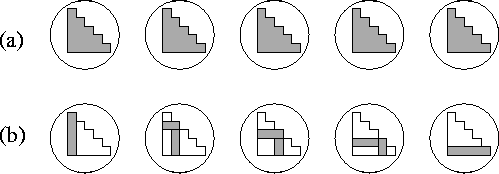
Figure 2.32: Agglomeration strategies for Fock matrix
construction with N=P=5 , for (a) the total replication algorithm and
(b) the partial replication algorithm. In each case, the five tasks are shown
with shading used to represent the portion of the symmetric D and
F matrices allocated to each task. In (a), each matrix is replicated in
each task. In (b), each task is given a single row and column; this corresponds
to a factor of two replication.
1. Total replication. Communication costs can be cut dramatically by replicating the F and D matrices in each of P tasks, one per processor of a parallel computer. Each task is given responsibility for 1/P of the integrals. Computation can then proceed in each task without any communication. The only coordination required is a final summation to accumulate partial F matrices. This can be achieved using a parallel vector reduction algorithm described in Section 11.2.
The technique of replicating data structures on each processor of a parallel computer is commonly used in parallel computing to reduce software engineering costs. It allows an existing sequential code to be adapted quickly for parallel execution, since there is no need to modify data structures. The principal disadvantage of the technique is that it is nonscalable. Because total memory requirements scale with the number of tasks created, the largest problem that can be solved is determined not by the total amount of memory in a parallel computer, but by the amount available in a single processor. For example, on a 512-processor computer with 16 MB of memory per processor, an implementation of the quantum chemistry code DISCO that uses this strategy cannot solve problems with N>400 . In principle, it would be interesting to solve problems where N is 10 times larger.
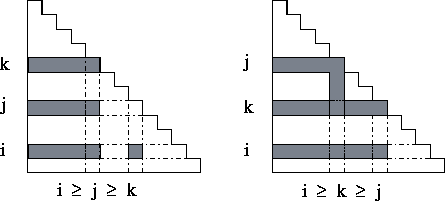
Figure 2.33: Data requirements for integral clusters.
Each task accesses three rows (and sometimes columns) of the D and
F matrices.
2. Partial replication. An alternative approach is as follows. First, we agglomerate computation in what seems an obvious
way, namely, by making the inner loop of the procedure fock_build in
Algorithm 2.3 into a
task. This yields 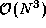 computation
tasks, each responsible for
computation
tasks, each responsible for 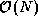 integrals. Next,
we examine the communication requirements of each such task. We find that there
is considerable locality in the data required by these clusters of integrals:
each cluster accesses the i th, j th, and k th row
(and sometimes column) of D and F (Figure 2.33). To
exploit this locality, we agglomerate data to create N data tasks, each
containing a row/column pair of the two-dimensional arrays D and
F and all of the one-dimensional array A. In this scheme, each
element of D and F is replicated once, and A is
replicated N times, so total storage requirements are increased from an
average of N to 3N per task. Because of this replication, each
computation task now requires data from just three data tasks. Hence, the number
of messages is reduced from
integrals. Next,
we examine the communication requirements of each such task. We find that there
is considerable locality in the data required by these clusters of integrals:
each cluster accesses the i th, j th, and k th row
(and sometimes column) of D and F (Figure 2.33). To
exploit this locality, we agglomerate data to create N data tasks, each
containing a row/column pair of the two-dimensional arrays D and
F and all of the one-dimensional array A. In this scheme, each
element of D and F is replicated once, and A is
replicated N times, so total storage requirements are increased from an
average of N to 3N per task. Because of this replication, each
computation task now requires data from just three data tasks. Hence, the number
of messages is reduced from 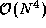 to
to 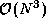 . The total volume
communicated remains
. The total volume
communicated remains 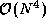 . Because the cost
of communicating a word is typically much less than the cost of computing an
integral, this is an efficient parallel algorithm.
. Because the cost
of communicating a word is typically much less than the cost of computing an
integral, this is an efficient parallel algorithm.
The ``partial replication'' Fock matrix construction
algorithm creates N data tasks and 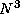 computation
tasks. We use the notation (i j k) to identify the computation task
responsible for computing the
computation
tasks. We use the notation (i j k) to identify the computation task
responsible for computing the 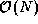 integrals
I
integrals
I 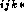 ; this task
requires data from data tasks i , j , and k . To
complete the parallel algorithm, we must define a mapping of data and
computation tasks to processors.
; this task
requires data from data tasks i , j , and k . To
complete the parallel algorithm, we must define a mapping of data and
computation tasks to processors.
We assume 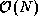 processors. Since
each data task will receive roughly the same number of requests, we allocate one
data task to each processor. This leaves the problem of mapping computation
tasks. We can imagine a variety of approaches:
processors. Since
each data task will receive roughly the same number of requests, we allocate one
data task to each processor. This leaves the problem of mapping computation
tasks. We can imagine a variety of approaches:
We have developed two alternative parallel algorithms for the Fock matrix construction problem.
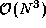 tasks, each
containing
tasks, each
containing 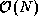 integrals.
These tasks are mapped to processors either statically or using a
task-scheduling scheme.
integrals.
These tasks are mapped to processors either statically or using a
task-scheduling scheme.
This case study illustrates some of the tradeoffs that can arise in the design process. The first algorithm slashes communication and software engineering costs; however, it is not scalable. In contrast, the second algorithm has higher communication costs but is highly scalable: its memory requirements increase only with problem size, not the number of processors. To choose between the two algorithms, we need to quantify their parallel performance and then to determine the importance of scalability, by assessing application requirements and the characteristics of the target parallel computer.
![[DBPP]](2_8 Case Study Computational Chemistry_files/asm_color_tiny.gif)





![[Search]](2_8 Case Study Computational Chemistry_files/search_motif.gif)
© Copyright 1995 by Ian Foster